Probabilistic data structures : Bloom Filter, Cuckoo Filter, Ribbon Filter

최근 시스템 설계 스터디를 하는중에 모르는 내용이 나와서 좀 찾아보게되었다.

확률적 데이터구조 (probabilistic data structures)

gpt 굿 그림이 조금 안맞긴한데 이게 가장 귀여우니까..

메모리와 성능을 절약하는 대신, 결과의 정확성에 약간의 오차를 허용하는 데이터 구조.
이런 데이터 구조를 갖는 대표적은 data structures들은 bloom filter, count-min sketch 등등이 있는데 그동안 이걸 왜 몰랐나 싶을정도로 아쉬웠다. 관심있는거만 공부하니까 그랬겠지...

Bloom Filter를 대표적으로 예를 들어보자.
우리가 프로그래밍적으로 Collection 안에 이 원소가 존재하는지(exist)를 확인하려면 보통 contains() 와 같은 메서드를 사용해서 결과를 가져오곤한다. 그런데 이 contains를 실행하기 위해서는 그 데이터 정보를 저장하기위해 O(n) 만큼의 저장공간 그리고 시간복잡도가 필요했는데, 이. Bloom Filter라는 확률적 데이터 구조를 사용하면 존재하는지 여부를 구하기 위해 원소들을 저장해야하는 많은 저장공간과, 이 원소가 존재하는지 찾아야하는 시간복잡도가 훨씬 줄어들게 된다. 그러나 이 결과값이 내가 설정한 오차값만큼 부정확할 수 있다.

즉 정확도를 버리는 대신, 공간과 시간 효율을 가져간 데이터구조이다.

그래서 이 확률적 데이터구조를 가진 여러 데이터구조들의 기능과, 정확도를 버리지 않았을 때. 실제 프로그래밍적으로 구현할 기능에 매핑시켜보면 아래와 같은 표로 매핑이 가능하다.

Data structure	기능	kotlin 스타일 함수
Bloom Filter	존재 여부 추정	contains(x)
Count-Min Sketch	빈도 추정	groupingBy{ it }.eachCount()[x]
HyperLogLog	고유 개수 추정 (cardinality)	distinct().count()
Top-K / HeavyKeeper	상위 K개 항목 추정	groupingBy{it}.eachCount().sortedByDescending().take(k)

위와 같은 Kotlin 스타일 함수를 보면 뭐.. 내가 원하는 기능을 하기위해 적당히 잘 구현되어있다. 근데 만약 이 안에 들어있는 데이터의 개수가 몇억, 몇백억, 몇천억과 같이 엄청나게 많다면? 이것들을 그냥 단순한 서버 메모리에 배열, 혹은 해시맵으로 저장하고, 성능좋게 탐색할 수 있을까? 아무래도 탐색시간도 오래걸리고, 기능에 비해 저장해야하는 메모리 용량도 많아질 것이다.

이때 이 확률적 데이터구조를 사용하면 데이터를 저장할 공간과 탐색 시간을 개선할 수 있다. 다만 그 결과값에 오차가 있을 수있다.
오차가 있는데 왜 사용하나? 싶을수있지만 어느정도 오차의 확률로 정확하기 때문에 완전한 정합성이 필요하지 않은 환경에서는 충분히 쓰일만 한것이다.

예를들면 유튜브 알고리즘 조회수가 몇개인지 검색하는 유저 입장에서 볼때 1의자리까지 꼼꼼하게 따져가면서 (정산제외) 보지 않고 우선 빠르게 그 값을 가져와야하는 상황과 같은 경우가 떠오른다.

외에도 실제로 데이터 엔지니어들이 많이 사용하는 Spark 프레임워크에서는 approx_count_distinct()와 같은 함수가 있는데 HyperLogLog 알고리즘을 기반으로 동작하고, 이는 정확하지는 않지만 상당히 근접한 고유값 개수를 작은 메모리로 빠르게 계산하기위해 사용하고 있다고 한다. (공부가 정말 부족하구나ㅠ) 실제로 많은 양의 데이터를 다룰 때 count()로는 3시간이 걸린다 치면
위 approx_count_distinct()를 사용하면 5분이 걸리는 식이라고한다.

따라서 성능이 중요한, 대규모시스템이라면 필요에 따라 이 확률형 데이터구조를 도입할수도 있을 것 같아 이 데이터 구조들이 동작하는 방식에 대해서 좀 찾아보게되었다.

 

Bloom Filter : 존재 여부 추정

Bloom Filter는 원소의 존재여부를 효율적으로 확인하는데 사용된다.
이 데이터구조는 1970년 Burton H. Bloom의 "Space/Time Trade-offs in Hash Coding with Allowable Error" 논문에서 처음 언급되었다. 

논문 : https://dl.acm.org/doi/10.1145/362686.362692

N = 비트 배열 / d = hash 함수의 개수

총 3가지 동작이 가능하다.

• INIT : 처음에 해시 영역의 모든 비트를 0으로 초기화한다.
• ADD : 그리고 저장할 각 메시지는 해시함수를 통과해서 나온 값을 (예: a₁, a₂, …, a_d) 이 값에 해당하는 비트 위치에 1을 설정한다.
• SELECT : 이렇게 저장된 상태에서 내가 원하는 메시지가 존재하는지 확인하려면, 그 메시지를 저장과 동일하게 d개의 해시값을 생성한다 (예: a₁, a₂, …, a_d) 이때 모든 비트가 1이면 이 메시지는 존재함이고, 하나라도 0인 비트가 있으면 존재하지 않음으로 판단한다.

그림으로 이해하는 Bloom Filter

이렇게 보면 모르기때문에 그림으로보자.
아래와 같이 N = 8, d = 3인 Bloom filter를 만들었다. 설명의 편의로 2차원 배열을 표현하였으나, 실제로는 해당하는 비트 위치에 1만 설정하므로 실제로 만들때 2차원 배열일 필요는 없다.

N = 8, d = 3 인 Bloom Filter

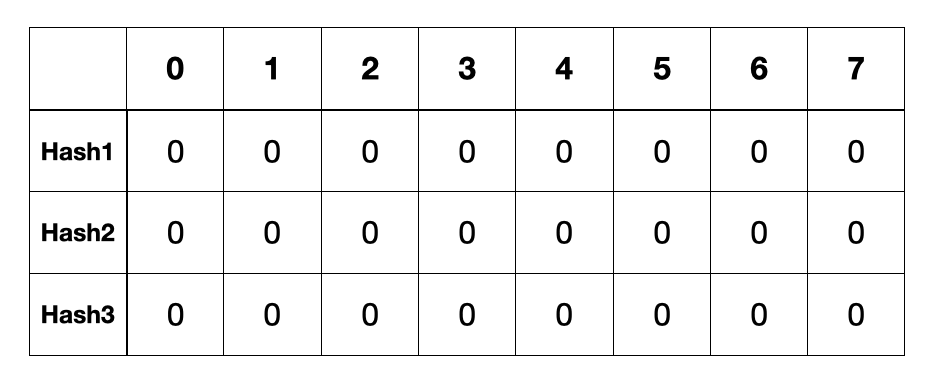
아래와 같이 이 Bloom filter에 메시지 a, b, c 를 추가한다.
a에 대해서 해시함수 Hash1, Hash2, Hash3각각을 통과시켰을때 그. 값이 1, 7, 5이므로 해당하는 비트에 1을 설정한다. 마찬가지로 b와 c도 각각 통과하여 비트에 1을 설정하는데, 이때보면 알겠지만 해시함수에 따라서 다른 메시지여도 같은 해시값을 가질 수 있다 (해시충돌) 이때에도 상관없이 1로 세팅한다.

마찬가지로 메시지 b와 c에 대해서도 저장하였다.

이렇게 저장되어있는 상태에서 이미 시나리오상 메시지 a만 존재하겠거니 알겠지만, 메시지 a, f 존재 여부를 보고싶을때 계산방법은

• a :  hash1(a) = 1,  hash2(a) = 7, hash3(a) = 5 각 위치의 비트가 모두 1 로 설정되어있으므로 a는 존재한다로 판단할 수 있다.
• f : hash1(f) = 1, hash2(f) = 3, hash3(f) = 4 각 위치의 비트가 모두 1로 설정되어있지 않아 f는 존재하지 않는다로 판단할 수 있다.
  이때 hash1(f) 가 hash1(a)와 동일한 값을 가져갔지만 다른 hash값을 이용해서 한번더 확인하므로 존재하지 않음을 판단하였다.

이상태로 메시지 g에 대한 존재여부를 보고싶어 추가로 계산해보았는데 이때 해시 충돌이 많이 난 상황이 발생하였다.

• g : hash1(g) = 1, hash2(g) = 5, hash3(g) = 3 각 위치의 비트가 모두 1로 설정되어있어 g는 존재한다로 판단할 수 있다.
  엇 그런데 여기서 이상하다. 우리는 g를 추가한적이 없는데 존재한다고 판단하였다. 

확률적 데이터구조인 이유가 바로 이 g에서 나온다. 확률상 정말 작겠지만 정말 만약의 사태로 내가 존재하지 않은 원소를 통과한 해시값의 비트가 전부 존재한다로 나오면 그 메시지는 존재하지 않음에도 존재한다고 (오차 발생) 결과가 나올 수 있기 때문이다.

즉, bloom filter는 false positive의 특징을 갖고있다. 1이면 존재할수있음. 하나라도 0이면 확실히 없음

논문에서의 이야기

직관적으로 보면 d값을 늘릴수록 오류확률(fraction of errors)는 줄어든다. 그러나 오류를 줄이겠다는 마음으로 d를 계속 증가시키면 일정 시점이후에는 수익체감지점(point of diminishing return)에 도달하게 된다. d를 1만큼 증가시키면 오히려 해시영역 전체에서 1이 된 비트의 비율이 더. 높아지는 현상이 발생한다고한다. 추가로 비교할 비트를 늘리는 효과보다 비트 하나를 무작위로 골랐을때 이미 1일 확률이 더 높아진다. 어쨌든 주어진 해시필드크기 N에 대해서 오류 확률의 이론적인 최소값이 존재한다고한다.

논문을 보면 이런 감각들에 대해서 수식으로 분석을 해둔걸 볼수 있었는데, (이 부분은 패스해도 된다)

기호	설명	수식	의미
N″	해시 영역의 전체 비트수	-	-
φ″	아직 0인 비트 비율	(1 - d / N″)^n	낮을수록 false positive 많아짐
P″	false positive 확률	(1 - φ″)^d
T″	평균 reject 시간	1 / φ″	reject 되기 까지 평균 몇개 비트 읽어야하는지

이런 수식을 따라 그러면 적절한 N의 값이 무엇일지 수식으로 표현한걸 보면 그 의미로

reject 시간을 고려하기위해 평균 T″비트만큼을 읽어야한다는 제약조건이 있을 때. falsePositive 확률 P″ 이하로 유지하기 위해서는 얼마나 큰 비트 N″이 필요한지를 계산할수있다는 것이다. 즉 이때 N″은 입력되는 값의 개수(n)에 비례함도 확인할 수 있었다.

즉 적은 false positive 확률P″를 가지면서 빠른 T″를 원한다면 N″은 커져야한다는 것이다.

논문에서는 이 Bloom filter를 불필요한 디스크 접근을 줄이는 사례로 접근했는데.

50만개의 단어를 처리한다고할때 90%는 간단히 rule based로 처리가 가능하지만 10%는 실제 사전을 참조해야하는 상황이라는 가정을 했하자. 이때 전체 10%는 디스크에 있는 사전에서 찾아야하는데 모든 단어에 대해. 디스크를 조회하는건 느리므로 이 10%만 Bloom Filter에 넣고 존재하지 않다고 나오면 넘어가고, 있을 가능성이 있을때 디스크로 확인한다를 시나리오를 세웠다.

이상황에 오차확률인 P 값을 매우 줄여보니 (그에 따른 Hash area가 늘어났음) 실제로 디스크 접근률이 매우 낮아짐을 알수있었다고한다.
즉 오차확률 약 1.5% 인 BloomFilter에 대해서 정확도 88%정도가 나왔음을 논문에서 이야기했다.

사실 1970년도 논문이라 이때는 disk 접근에 대한 부담이 있어서 이런 방법을 소개한것 아닐까 싶은데 이걸 시작으로 지금까지도 확률적 데이터구조가 시작되게 되어서 좀더 보게되었다. 따라서 Bloom filter 데이터 구조를 가져갈 때 약간의 오류(false positive)를 허용하면 작은공간으로도 빠른 테스트가 가능하다는 점을 알 수 있다. 대용량 데이터를 처리하는 시스템에서 아무래도 많은 이점을 가져갈 수 있다.

비트 N″ 값에 대한 의문

처음 이 Bloom Filter 개념을 접했을때 가장 이해를 못했던 부분은 왜 비트의 값이 INT.MAX, LONG.MAX가 아니지? 라는 의문이었다. 그동안 프로그래밍을 하면서 해시함수의 return 값이 보통 int니까. 그 비트배열의 크기는 항상 INT.MAX 아닌가? 하는 너무나도 현대 프로그래머적인 생각을 했다. 그런데 이 논문을 읽고보니 (gpt에게 한글로 설명해줘..) 이때는 메모리 할당을 하나하나 하던 시절이었을테니 그랬던 것으로 이해를 했고. 실제로 이 N 값은 아무리 해시 함수의 return 이 Int 여도 조절이 가능한 값이긴 했다.

int hashValue = hashFunction(x);
int columnIndex = hashValue % N;

실제 메모리 사용량을 조절하기 위해 내가 원하는 N값으로 modular를 하는 방법을 취할 수 있기 때문이다.

실제로 이 확률적 데이터 구조를 사용하지 않으면 n개의 원소를 저장한다고할 때, 원래는 공간복잡도 O(n)만을 차지할 것이다. 그러나 이 확률적 데이터구조를 사용하면 해시함수의 개수인 O(d) 만큼만을 차지해도 n개의 원소에 대해서 false positive를 알 수 있는 상황이라 대규모 시스템에서 공간적 이점을 매우 크게 가져갈 수 있음을 이해하게 되었다.

 

Redis Probabilistic Data Strucutures

실제로 사용하고싶으면 이 bloom filter 로직을 내가 직접 짜야하는건가? 절대 아니다 1970년도 논문인데 그에 따른 라이브러리 하나 없을까. 가장 대표적으로 redis에서 이미 Probabilistic data structures를 설명 및 제공하고 있다.

 

https://redis.io/docs/latest/develop/data-types/probabilistic/bloom-filter/

Bloom filter

실제 Redis를 이용해서 Bloom Filter를 사용할때는 오차율(error_rate)을 기반으로 정의하는 방식을 사용하고있다. 위의 설명을 위해 예시를 든 것처럼 hash 함수의 개수인 d값을 미리 정의하는 방식이 아님을 알고 넘어가자. 아무래도 개발자가 직접 d값을 조정하는것보다 오차율을 낮추는게 더 중요하다고 판단한 것으로 보인다.

일반적인 redis 서버만으로는 위 Bloom Filter 데이터구조를 사용할 수 없다. 추가적인 모듈을 사용해야하는데 아무래도 귀찮아서 이미 제공되어있는 도커 이미지를 사용했다.

docker run -d --name redis-stack -p 6379:6379 redis/redis-stack-server:latest

redis-cli를 이용하여 bloom filter를 손쉽게 사용할 수 있다.RESERVE command를 이용해서 오차 확률과 예상 원소수를 설정하면 그에 맞게 bloom filter가 세팅되는데 그 정보 역시 BF.INFO 커맨드로 확인이 가능하다. 위의 EXISTS 결과를 보면 알듯이 false positive임을 확인할 수 있다. (실제로 넣지 않은 a값에 대해서 true로 리턴함.) 이는 의도적으로 오차율을 높게 설정하고, 예상 원소수를 낮게 설정했기 때문에 발생하였다.

따라서 redis로 bloom filter를 사용할 때 의도적으로 오차율을 낮게 설정하는것도 가능하니 정확도가 중요하다면 이 error_rate와(오차율) capacity(예상 원소수)을 잘 설정하도록하자. INFO로 확인했을때 확실히 오차율을 줄이기 위해 size가 크게 잡힌걸 볼 수 있다.

BF.DEBUG를 사용하면 byte레벨의 좀더 자세한 정보를 알 수 있다.

참고하면 좋은 자료

• https://redis.io/docs/latest/operate/oss_and_stack/stack-with-enterprise/bloom/commands/#bloom-filter-commands
• https://redis.io/blog/bloom-filter/
• https://github.com/RedisBloom/RedisBloom/blob/master/src/rebloom.c#L132

 

확장버전 Bloom Filter 

1970년도 논문인만큼 그에 따른 확장버전도 굉장히 많이 나왔다. 위에 참조한 redis 사이트에서도 가장 원시적인 Bloom Filter 외에도 Scalable Bloom filter, Cuckoo Filter를 함께 제공하고 있음을 볼 수 있다.
찾아보다가 우리학교 동문들이 게제한 논문도(터너리 블룸필터) 있어서 반가웠고 논문 설명처럼 실제로는 network 전송에서 사용하는 알고리즘으로 많이 고려된다는 점을 알 수 있었다. 

구조	기능 확장	핵심 특징
Counting Bloom Filter	삭제 지원	각 비트를 카운터로 바꾼다 (1비트 → k비트).
Scalable Bloom Filter	크기 자동 확장	false positive 한계 초과 시 새 Bloom Filter 추가
Compressed Bloom Filter	압축 저장	네트워크 전송/저장용 최적화
Cuckoo Filter	삭제 + 정확도 개선	Cuckoo Hashing 기반. 실제 key의 fingerprint 저장
Ribbon Filter (Facebook)	압축 + 빠른 쿼리	XOR 기반의 경량 구조, 매우 작은 false positive
Xor Filter (Google)	고정된 key 집합	Perfect hashing 기반, 매우 빠르고 compact

Counting Bloom Filter(2010년 논문)의 경우엔 기존에 해당하는 비트를 1로 세팅하는게 아니라 각 비트에 대해서 카운터로 바꾸는만큼 실제 2차원 배열로 만들어서 저장해야하는 특징이 있고, add 할 때 마다 해당하는 비트의 값에 +1을 하고, 삭제를 위해서는 -1을 하는 방식으로 동작한다. 이렇게만봐서는 사실 Count-Min Sketch와 비슷한 점이 있지만 사용 목적과 쿼리의 의도가 다르기 때문에 그 안의 데이터구조 (실제 N과d)가 다를 수 있기 때문에 구분해야할 것이다.

Scalable Bloom Filter(2007년 논문)는 더 많은 아이템을 넣을 수 있도록 새로운 Bloom Filter를 추가하고 계층을 추가하는 방식이다. 이렇게 추가된 계층은 해시 함수의 개수(d)는 동일하게 가져가고 비트배열의 너비(N)을 더 크게 가져간다. 해시는 어차피 같은것을 사용하므로 모든 계층에 대해서도 모두 존재하지 않는지 미리 확인하고 현재 필터에 추가하는것이다. 그러나 더 많은 레이어를 가져감으로인해서 많은 용량을 쓰게됨으로 성능이 크게 저하된다. 따라서 Scalable이라 해도 포함할 항목수(n)을 정확히 아는게 중요하다.

또한 위의 Redis Bloom Filter의 경우 Scalable Bloom Filter를 사용하는 걸 옵션으로 제공하고 있다.
실제로 위에서 사용한 error_rate 0.5 capacity 10 예제에서 더 많은 원소를 추가하고 INFO를 했더니 Number of filters 값이 1에서 2로 늘어나고, size도 104에서 184로 늘어남을 확인할 수 있었다.

좌 : 원소를 capacity 이상으로 넣기 전. / 우 : 원소를 capacity 이상으로 넣은 후

Compressed Bloom Filter(2002년 논문)는 똑같이 일반 Bloom Filter처럼 해시해서 비트를 설정하되 이 비트배열을 압축과정이 추가된다.

Cuckoo Filter

BloomFilter는 해시함수의 값에 위치한 비트를 1로 만드는 비트 배열인 특징이 있지만, Cuckoo Filter는 버킷배열로 문제를 해결했다. Bloom Filter가 삭제를 지원하지 않는다는 점과, Counting Bloom Filter는 삭제는 가능하지만 메모리를 더 많이 사용하여 성능저하가 발생가능하다는 문제점을 기반으로 시작되어 이런점을 개선하였고 실제로 성능도 더 좋아졌다.

Cuckoo Filter의 내용은 2014년에 저술된 "Cuckoo Filter: Practically Better Than Bloom"논문에서 소개되었다.
논문: https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf

Cuckoo Hashing을 기반으로한 동작방식

기본적으로 Cuckoo Hashing을 기반으로 작동하며 bloomFilter에서 각 비트 배열의 인덱스를 1로 설정했던 방식이 아니라 item의 fingerprint를 버킷에 삽입하는 방식이다. 그리고 충돌하면 evict 후 relocation하는 방식이다.

1. 두 버킷 중 하나에 빈 자리가 있으면 삽입
2. 둘 다 차 있으면, 기존 아이템 하나를 쫓아내고(evict) 재 삽입(relocation)
3. 이 과정은 빈 공간이 생기거나 최대 재시도 횟수에 도달할 때까지 반복

이 fingerprint는 입력값 전체가 아니라 이 입력값의 해시값의 일부만 저장하는 것을 의미하며 덕분에 메모리 사용량도 적어지고 삭제도 가능해진다고 한다. (이건 좀더 아래에서 알아보자)

insert 방식과 간략한 데이터 구조를 이해하기 위해 아래의 visualization 툴을 사용하여 테스트해보면 이해가 빠르다.

https://www.lkozma.net/cuckoo_hashing_visualization/

Cuckoo Hashing Visualization :: Laszlo Kozma

 

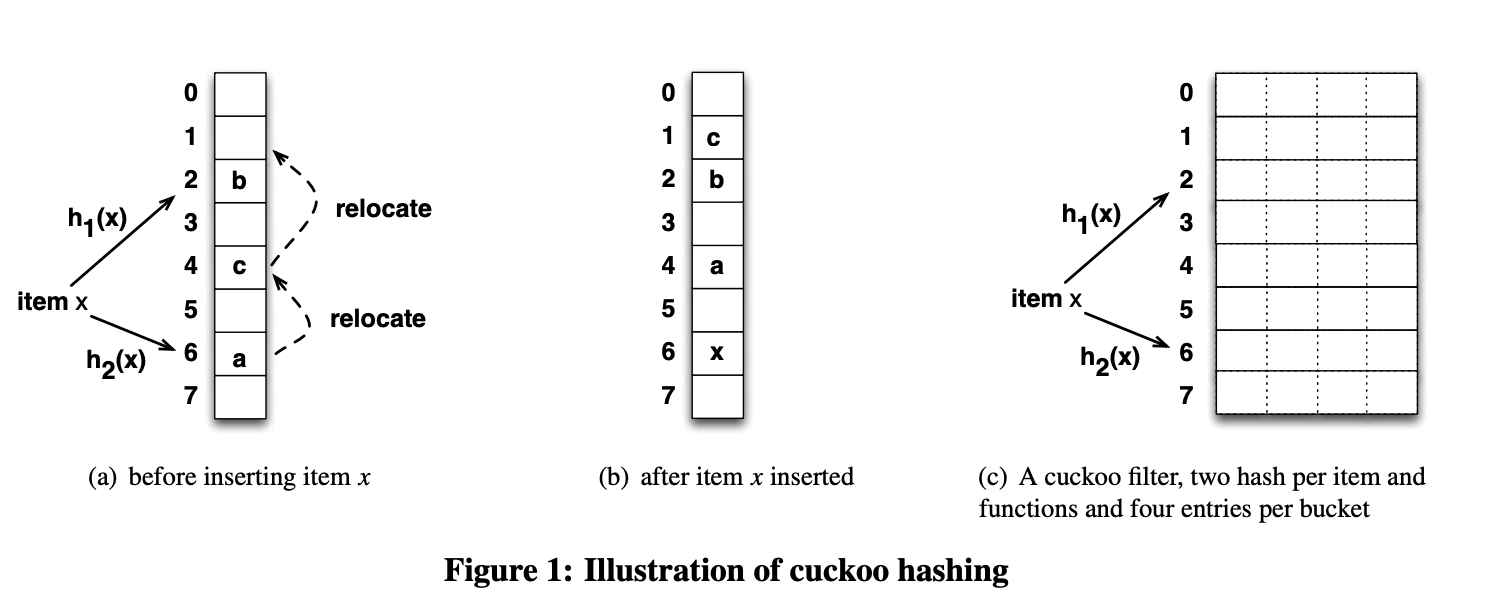
논문에 나온 내용을 기반으로 insert 시나리오를 정리한다. 이때는 item 자체를 insert한다고 생각하자.

• a) item x를 삽입하려고하는데 h1(x), h2(x) 의 결과에 해당하는 2번 6번 버킷이 이미 차있는 상황이다. 이런상황에서 a가 위치한 6번 버킷을 evict 하기로 결정한다. a가 evict되었기 때문에 a는 relocate가 필요한 상황이라 h1(a), h2(a)의 결과를 찾고 그 결과 현재 버킷의 위치가 아닌 다른 버킷의 위치인 4번으로 relocate한다. 그러나 그 결과 4번에 있던 c는 evict가 필요한 상황이다. 마찬가지로 c도 h1(c), h2(c)의 결과를 찾고 그 결과 현재 버킷의 위치가 아닌 1번으로 relocate 한다.
• b) relocate과정이 끝나서 삽입하려고 한 x의 위치는 6번 버킷에 잘 들어가있고 relocate의 최종 결과로 a는 4번, b는 2번, c는 1번 버켓에 위치하게 되었다.
• c) cuckoo filter에서는 이런 각 버킷이 b개의 엔트리를 가질 수 있다. 아무래도 cuckoo filter는 해시 충돌 발생시에 eviction으로 빈 공간을 찾는데, 버킷당 엔트리가 1개라면 위의 a,b 과정처럼 evction + relocation 과정이 매우 많아져 성능 저하가 발생할 수 있기 때문이다. 따라서 버킷당 여러 엔트리를 허용함으로써 삽입 성공률 증가, evction 감소를 노린 것이다. 따라서 같은 bucket index를 갖더라도 버킷안에 여러개의 entry를 두는 방식으로 더 안정적인 성능을 가져가게 되는 것이다.

또한 위의 visualization으로 테스트를 하다보면 결국 entry가 적은경우엔 evction > relocation이 무한루프를 도는 경우가 생기게된다. 마치 위의 a,b 시나리오에서 더이상 삽입할 공간이 없는것과 같다. 이런경우를 대비해서 cuckoo filter는 최대 retry 횟수를 가지고있으며, 이 최대 retry 횟수를 넘어가게되면 무한루프를 끊고 insert 불가능을 알려 bucket자체의 entry를 늘린다거나 bucket의 크기를 늘린다거나 등의 조치를 취하도록 유도한다.

fingerprint와 partial-key cuckoo hashing

위에 잠깐 언급하였지만 cuckoo filter는 공간 효율을 높이기 위해 아이템을 hash table내에 전체 데이터를 저장하지 않고, fingerprint(해시 요약값)만 저장하여 메모리를 줄이는 방법을 사용하였다. 따라서 insert시에 fingerprint 값 만으로 버킷 후보의 위치를 결정하게되는데, 문제는 이때 eviction이 되게되면 이미 fingerprint값만 갖고있어서 다시 원본키로부터 alternate 위치를 구할 수가없다.

따라서 이때 partial-key cuckoo hashing기법을 추가로 사용한다.

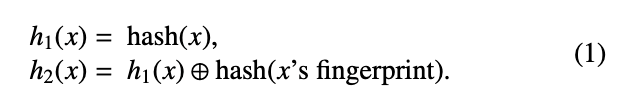
fingerprint의 해시값과 현재 위치를 xor하여 다른 alternate 버킷의 인덱스를 알 수 있게된다.

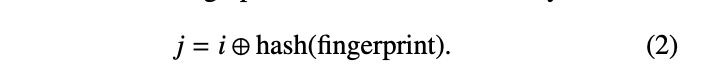
따라서 원래는 h1 hash, h2 hash 별도로 있다고 가정하고 cuckoo filter를 사용했으나, fingerprint만으로 insert 했을때 문제점 해결을 위해 h2 hash를 h1기반으로 만들게 된 것이다. 그럼에도 XOR을 사용했기 때문에 bucket이 인접하게되는것을 방지해 충돌을 줄일 수 있는 해시라고 판단한 것으로 보인다. (만약 8-bit fingerprint를 사용한다면 최대 256 (= 2^8)개 떨어진 위치로 relocation 가능하기 때문이다.

그렇기 때문에 역시 partial-key cuckoo hashing의 문제점은 있는데

1. 해시값의 조합 수 감소
   표준 cuckoo hashing 자체는 h1, h2를 다른 함수로 생성하지만 partial-key hashing은 기존 h1을 활용하는 방식이다.
   따라서 h1, h2 조합의 가지수가 줄어들수밖에 없고 충돌 확률 증가 가능성이 있다.
2. 동일한 fingerprint를 갖는 서로 다른 아이템 insert 문제
   서로 다른 item x, y가 같은 fingerprint를 가질수있다. 따라서 이때 같은 버킷안에 fingerprint가 여러번 등장하는것도 가능하다. 그러나 같은 아이템이 2b번 이상 삽입되는 경우 (b = 버킷당 슬롯수) 두 버킷이 모두 가득차셔 overflow가 발생할 수 있다.

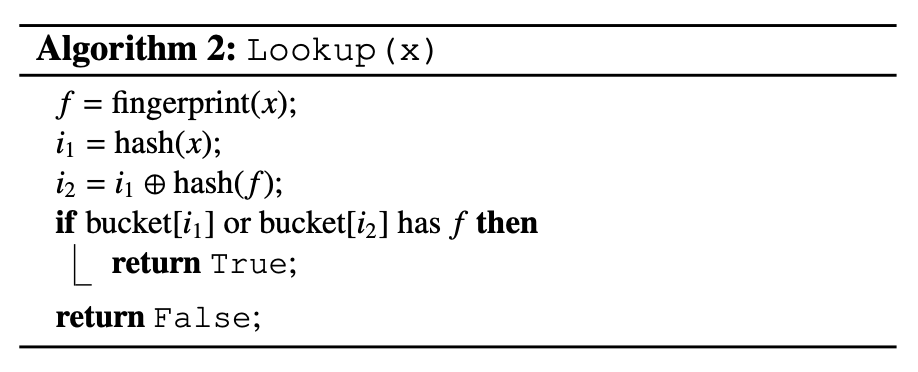
논문에 있는 알고리즘을 가져온 것이다

조회는 정말 간단하다. 두개의 버킷을 계산해서 두 버킷중 하나에 fingerprint가 존재하면 존재함으로 간주한다.
따라서 이때는 false negative가 적용된다 (존재하는데 없다고 나오는 경우)가 없음. bloom filter와 비슷하게 다른 item인데 같은 해시값의 버킷을 갖는경우가 있다면 발생할 수 있기 때문이다.

삭제도 간단하다. 두 버킷중 하나라도 fingerprint가 존재하면 존재하는 버킷에서 삭제만 하면 끝이다. 다만 위의 조회와 마찬가지로 fingerprint만 비교하기 때문에 x와 동일한 fingerprint를 가진 다른 아이템일 수도 있다는 점을 주의해야한다. (x, y가 같은 fingerprint일때 x를 삭제해도 y가 남아있다면 여전히 x가 존재한다고 나올 수 있다.)

실제 효율에 대한 결과

따라서 이런 cuckoo filter를 사용할 땐 서로 상관관계를 값들이 정말 많다. 논문의 실험 내용을 몇개 가져오자면

1. fingerprint 길이에 대한 분석

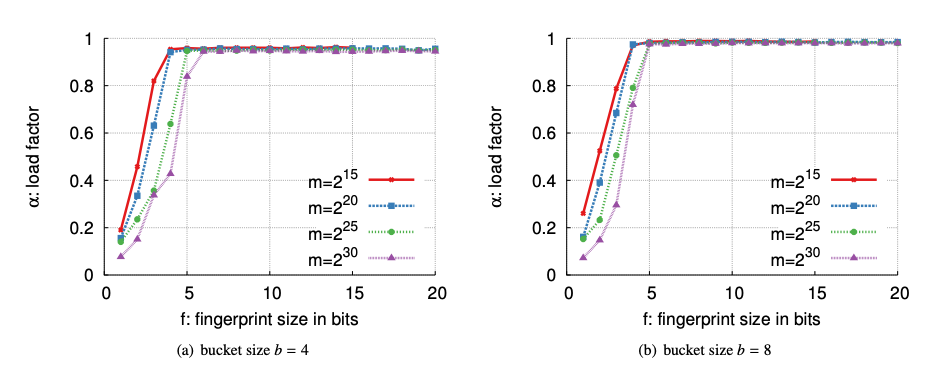
- load factor = 용량 대비 데이터가 어느정도 찼을 때 사이즈 확장이 필요한지를 판단할때 쓰이는 값
- bucket size = 위에서 말한 entry size, 즉 한개의 bucket에 허용하는 entry
- m = bucket의 개수 ( 테이블크기)

fingerprint의 비트가 늘어나면 아무래도 item 자체의 식별할 수 있는 비트의 개수가 늘어남으로 그만큼 false positive는 감소한다.
그러나 위 그래프와 같이 entry의 개수가 4일때나 8일때나 95%, 98%로 load factor 자체 대세에는 큰 영향을 주지 않았다.
entry의 크기 자체는 높을수록 load factor가 높아지지만 lookup시 체크해야할 슬롯이 많아진다.
또한 bucket의 개수는 커질수록 더 큰 fingerprint가 필요함을 보였다. 충돌방지를 위해 약간 더 긴 fingerprint가 필요하다. 

따라서 6~8비트의 fingerprint만으로도 높은 채움률을 달성함을 보여줬다. 길이의 적정값을 채움으로써 효율적인 동작을 실험한 셈이다.

2. 공간 최적화 실험 (space optimization)

교차점 3%가 중요한데, 3%보다 낮은 false positive를 요구하면 cuckoo filter가 공간효율이 더 좋고, 아닌경우엔 bloom filter가 공간효율이 좋다는 의미이다. 보라색의 lower bound는 어떤 확률 자료구조라도 이 하한아래로는 갈수없음을 의미한다.

즉 3%의 false positive충족하는 지점의 경우 아이템 하나 저장에 7.2bit를 사용한다는것인데, 이 값보다 false positive를 낮추고싶다면
bloom filter는 더 많은 비트가 필요하기 때문에, cuckoo filter가 그보다 더 낮은 비트를 사용함으로 공간효율적이라는 이야기를 할 수 있다는 것이다.

이외에도 많은 내용이 있어보이나... 패스

추가로 보면 좋을 것은 redis에서도 이런 공간효율이나 삭제가능성 기능 덕분에 bloomfilter와 cuckoofilter를 구분해서 제공하고있다. error rate계산에 따라 알아서 공간할당을 해주고있으니 실제로 cuckoo filter를 사용하고싶다면 redis io 코드를 참고하는 것도 방법이다.

참고하면 좋은 자료

• https://redis.io/docs/latest/develop/data-types/probabilistic/cuckoo-filter/#interesting-facts
• https://levelup.gitconnected.com/cuckoo-hashing-a-beginners-guide-e010288bf05d

 

Ribbon Filter

그리고 마지막으로 Facebook에서 만든 Ribbon filter가 눈에 띄었는데, 2021년에 논문을 게제한 만큼 최신이다.

https://engineering.fb.com/2021/07/09/core-infra/ribbon-filter/

Ribbon filter: Practically smaller than Bloom and Xor

아무래도 Bloom Filter와 Xor Filter보다 더 작고 빠른 필터임을 내세우고 있는데, XOR Filter자체는 cuckoo filter와 다른것이며 삭제는 불가능하지만 공간효율이 bloom filter에 비해 좀더 좋은 성능을 좋은 자료구조이다. 따라서 Ribbon filter가 내세우고자 하는 것은 삭제가 안되는 filter들 중에서 본인이 가장 공간효율이 좋음을 이야기하는 것이다. 그러나 삭제가 불가능하기 때문에 대용량 읽기 전용 환경에서만 적합하다는 점을 꼭 짚고 넘어가자.

위의 engineering blog에서 이야기하는 장점으로는 O(1)의 쿼리시간 Bloom filter에 비해 1/3의 메모리 절약이 있다는 점이다. 
또한 성능상으로 중요한 지표인 아래 4가지가 간단한 api뒤에 감쳐져서 원하는대로 조절이 가능하다.
1. number of keys 2. memory usage 3. CPU efficiency, 4. accuracy 

Ribbon Matrix 라는 행렬을 사용하는데 이게 물리적으로 리본처럼 보이기 때문에 ribbon filter라는 이름이 붙게 되었다.

 

마무리

리본필터의 내용은 여력이 되면 나중에 좀더 공부해보려한다.
아무래도 이걸 보기위해 논문 gpt에 넣고 이해하고 다시 물어보고하면서 공부하다보니 점점 뇌절하는 느낌이라
여튼 SWE 입장에서는 확률적 데이터 구조를 사용하여 작은 공간을 가지면서도 빠른 false positive로 DB접근을 줄여 효율성을 높이는 방향이기 때문에 대용량 시스템에서 유용하게 사용할 수 있을 것으로 보여 관심을 갖게되었다. 사실 시스템설계 스터디에서 본건 Count-min sketch 에 대한 내용이었는데 이 내용도 이해한 내용들을 추가로 정리할 예정이다. 끝!